K Nearest Neighbor(KNN) is a very simple, easy to understand, supervised machine learning algorithms. KNN classifier classifies new data in a particular class based on a similarity measure

How does KNN works

A new observation is classified by a majority of its neighbors If K=1, then the class is simply assigned to the class of its nearest neighbor

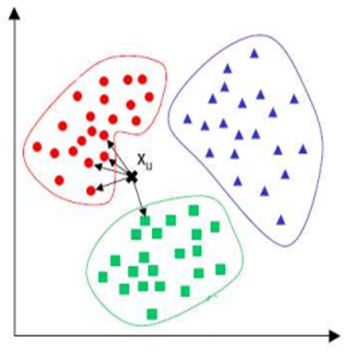
Requires three things

• The set of stored records
• Distance Metric to compute distance between records (for example the Euclidean distance)
• The value of k, the number of nearest neighbors to retrieve

To classify an unknown record:

• Compute distance to other training records
• Identify k nearest neighbors
• Use class labels of nearest neighbors to determine the class label of unknown record (e.g., by taking majority vote)

KNN implementation with Scikit-Learn

Importing Libraries

import numpy as np import matplotlib.pyplot as plt import pandas as pd

Importing the iris dataset.

url= "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']

# Read dataset to pandas dataframe
dataset = pd.read_csv(url, names=names)

Let’s display the five first records. Each observation represents one flower (class value) and 4 columns represents 4 measurements

 dataset.head() 

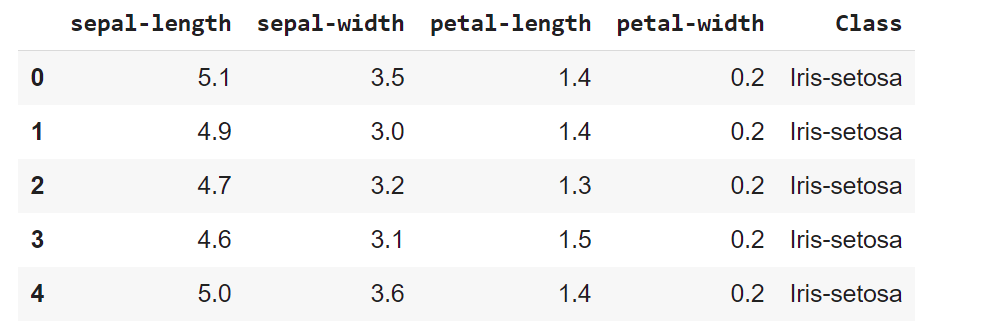
The next step is to split our dataset into its attributes and labels

 X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values

Split the data into training and testing sets

To evaluate the model performance we need to divide the dataset into a training set and a test set. This way our algorithm is tested on un-seen data, as it would be in a production application.

Let’s split dataset by using function train_test_split(). You need to pass 3 parameters features, target, and test_set size.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20)

Data standardization

As the KNN is based on calculation distance measures, it’s better to standardize the data

from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)

X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)

Runnin the training and prediction

Let’s build KNN classifier model for k=5.

from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=5)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)

Model Evaluation

There are different measures to evaluate the performance of a classification algorithm as the accuracy, confusion matrix, precision, recall and f1 score. Let’s estimate, how accurately the classifier can predict the type of the flowers. Accuracy is the most intuitive performance measure and it is simply a ratio of correctly predicted observation to the total observations. Accuracy can be computed by comparing actual test set values and predicted values

 
#Import scikit-learn metrics module for accuracy calculation
from sklearn import metrics
# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

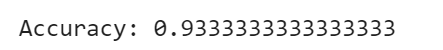
Let’s fit and test the model for different values for K (from 1 to 40) using a for loop and record the KNN’s testing accuracy in a list variable (error).

error = []

# Calculating error for K values between 1 and 40
for i in range(1, 40):
    classifier = KNeighborsClassifier(n_neighbors=i)
    classifier.fit(X_train, y_train)
    pred_i = classifier.predict(X_test)
    error.append(metrics.accuracy_score(y_test, pred_i))

Plot the relationship between the values of K and the corresponding testing accuracy using the matplotlib library. As we can see there is a raise and fall in the accuracy

 from matplotlib import pyplot as plt
plt.plot(error)
plt.show()

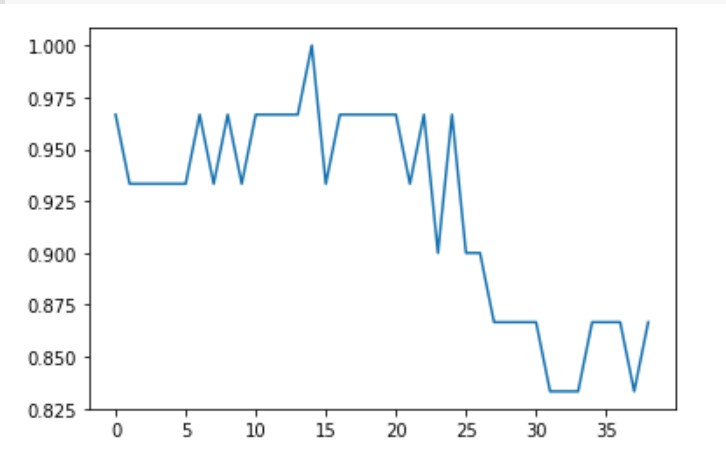
In KNN, finding the value of k is not easy. A small value of k means that noise will have a higher influence on the result and a large value make it computationally expensive. Some researchers recommand to set k=sqrt(n), where n is the dataset size.

---

You probably got different results from what you see here. This is because dataset splitting is random by default. The result differs each time you run the function. However, this often isn’t what you want.

Sometimes, to make your tests reproducible, you need a random split with the same output for each function call. You can do that with the parameter random_state. The value of random_state isn’t important—it can be any non-negative integer. You could use an instance of numpy.random.RandomState instead, but that is a more complex approach.

X_train, X_test, y_train, y_test= train_test_split(X, y, test_size=0.20,random_state=4)